
Did you know that the two sample t test is used to calculate the difference between population means?

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)
Now, there 3 ways to calculate the difference between means, as listed below:
Let’s find out more!
So how do we compare the mean of some quantitative variables for two different populations?
If our parameters of interest are the population means, then the best approach is to take random samples from both populations and compare their sample means as noted on the Engineering Statistics Handbook.
In other words, we analyze the difference between two sample means to understand the average difference between the two populations. And as always, the larger the sample size the more accurate our inferences will be.
Just like we saw with one-sample means, we will either employ a z-test or t-test depending on whether or not the population standard deviation is known or unknown.
However, there is a component we must consider, if we have independent random samples where the population standard deviation is unknown – do we pool our variances?
When we found the difference of population proportions, we automatically pooled our variances. However, with the difference of population means, we will have to check. We do this by finding an F-statistic.
If this F-statistic is less than or equal to the critical number, then we will pool our variances. Otherwise, we will not pool.
Please note, that it is infrequent to have two independent samples with equal, or almost equal, variances — therefore, the formula for un-pooled variations is more readily accepted for most high school statistics courses.
But it is an important skill to learn and understand, so we will be working through several examples of when we need to pool variances and when we do not.
For example, imagine the college provost at one school said their students study more, on average than those at the neighboring school.
However, the provost at the nearby school believed the study time was the same and wants to clear up the controversy.
So, independent random samples were taken from both schools, with the results stated below. And at a 5% significance level, the following significance test is conducted.
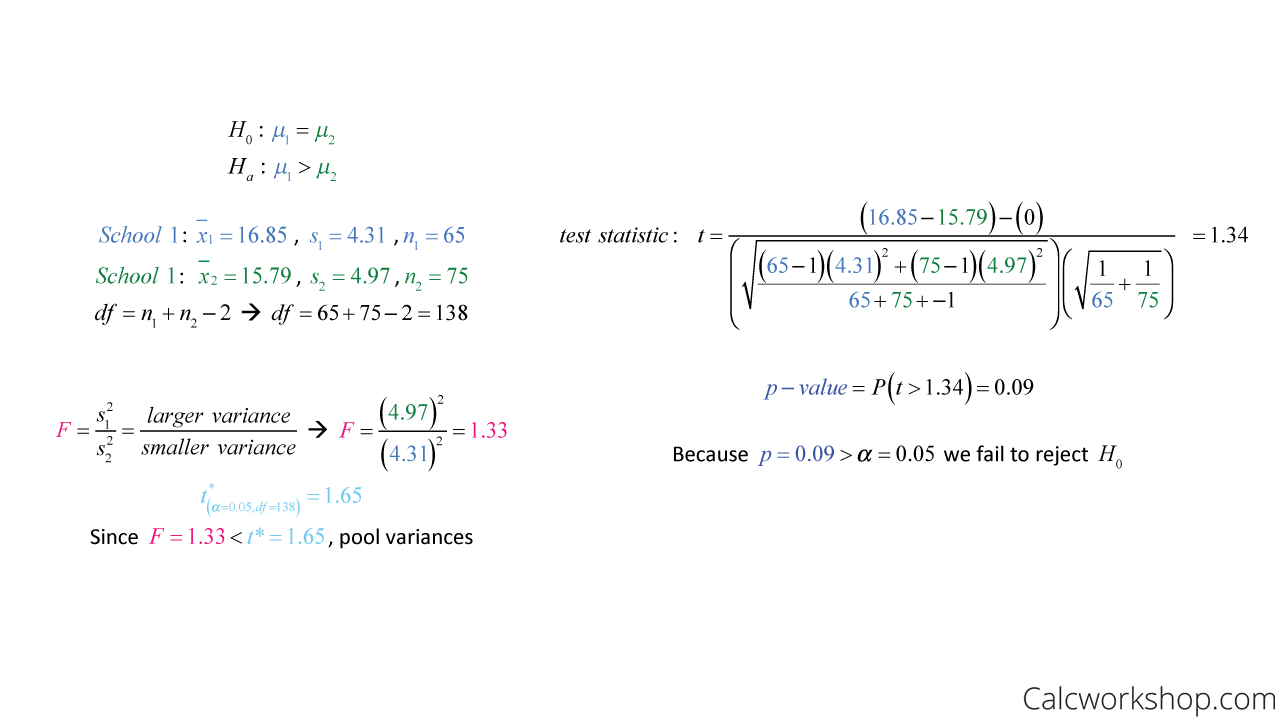
Two Sample T Test Pooled Example
Notice that we pooled our variances because our F-statistic yielded a value less than our critical value. The interpretation of our results are as follows:
But what do we do if the populations we wish to compare are not different but the same?
Meaning, the difference between means is due to the population’s varying conditions and not due to the experimental units in the study.
When this happens, we have what is called a Matched Pairs T Test.
The great thing about a paired t test is that it becomes a one-sample t-test on the differences.
This means we will first find the differences between the two treatments.And then we will calculate the sample mean and sample standard deviation, sometimes referred to as standard error, using these difference values.

Matched Pairs T Test Formula
What is important to remember with any of these tests, whether it be a z-test or a two-sample t-test, our conclusions will be the same as a one-sample test.
For example, once we find out the test statistic, we then determine our p-value, and if our p-value is less than or equal to our significance level, we will reject our null hypothesis.

One Sample Flow Chart
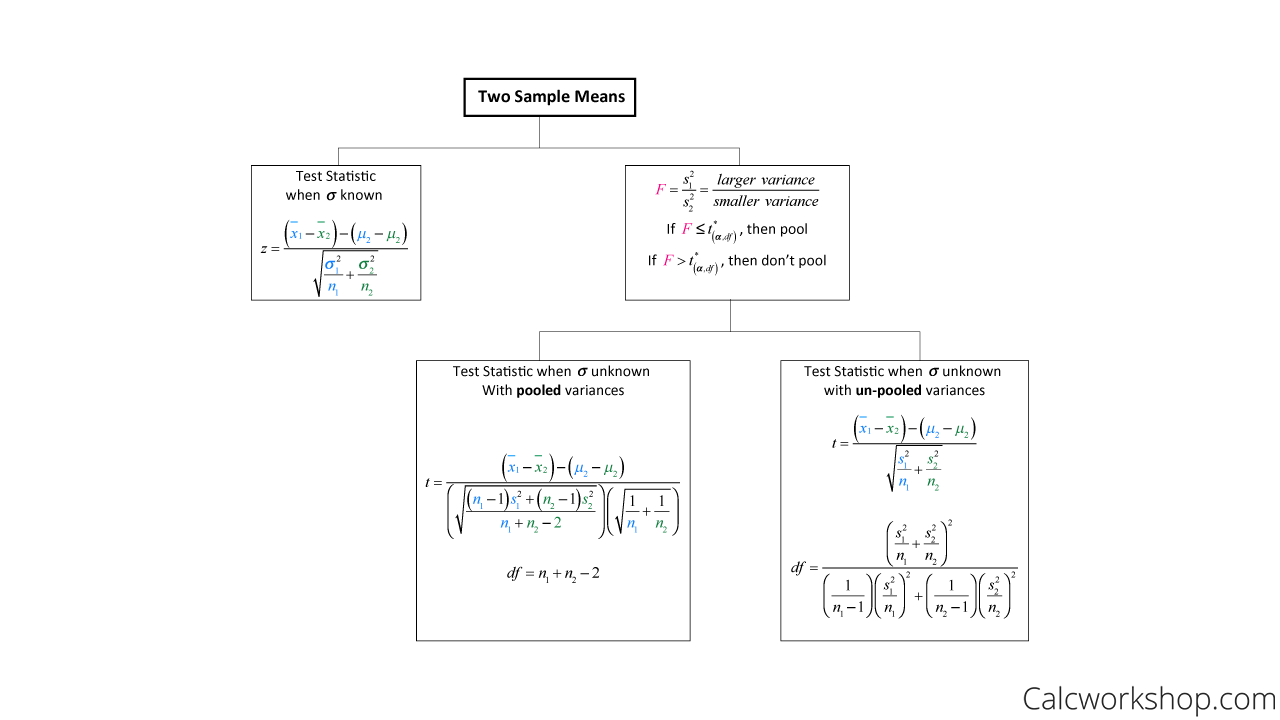
Two Sample Flow Chart
As the flow chart demonstrates above, our first step is to decide what type of test we are conducting. Is the standard deviation known? Do we have a one sample test or a two sample test or is it matched-pair?
Then, once we have identified the test we are using, our procedure is as follows:
Together, we will work through various examples of all different hypothesis tests for the difference in population means, so we become comfortable with each formula and know why and how to use them effectively.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.